√ 最小 公倍数 問題 161303-分数 最小 公倍数 問題
最小公倍数から自然数を決定する問題 ヒロ まずは自然数が2つの場合から練習しよう。 問題 n と16の最小公倍数が144であるような自然数 n をすべて求めよ。 考え方と解答 16と144をそれぞれ素因数分解して,どのような素因数をもっているかを
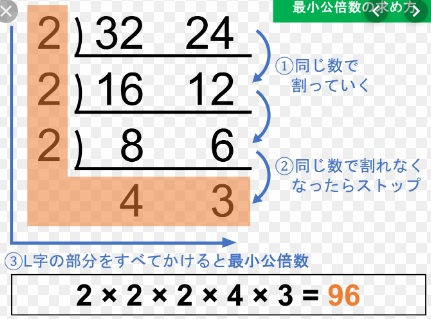
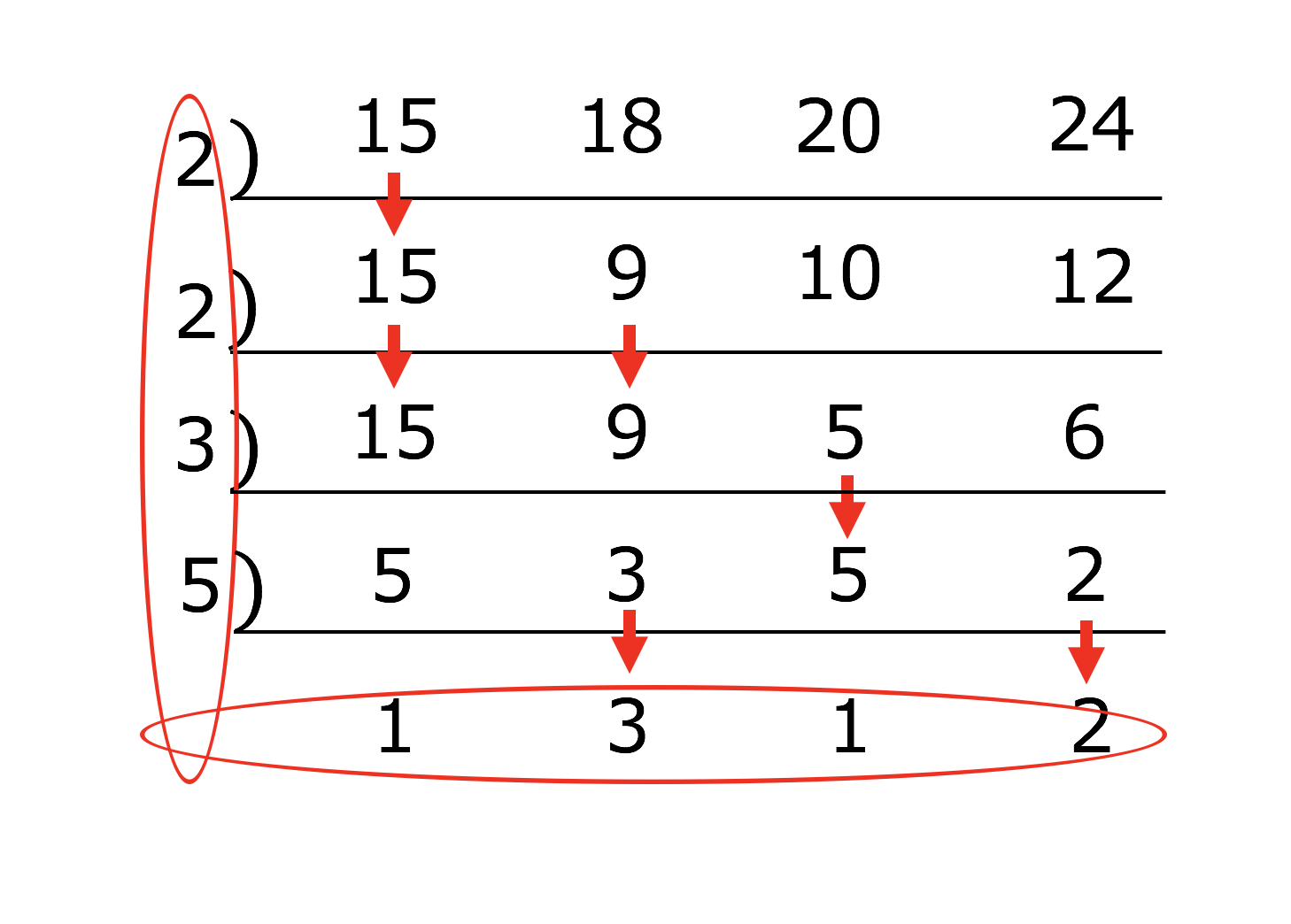
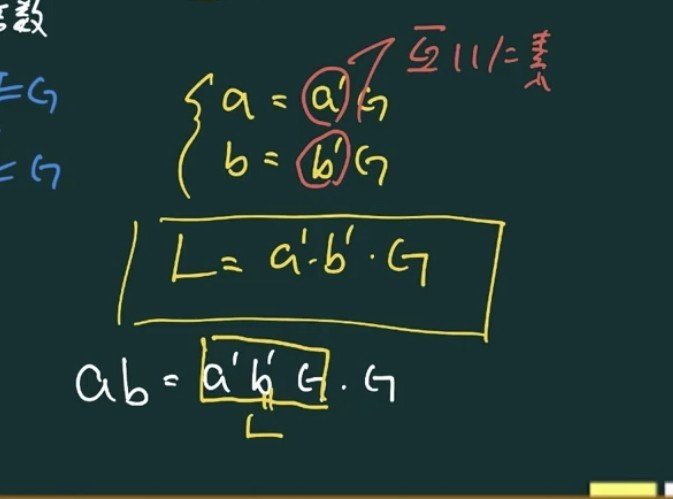
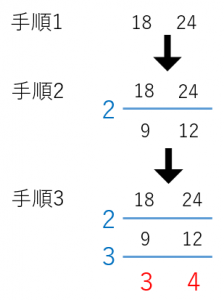
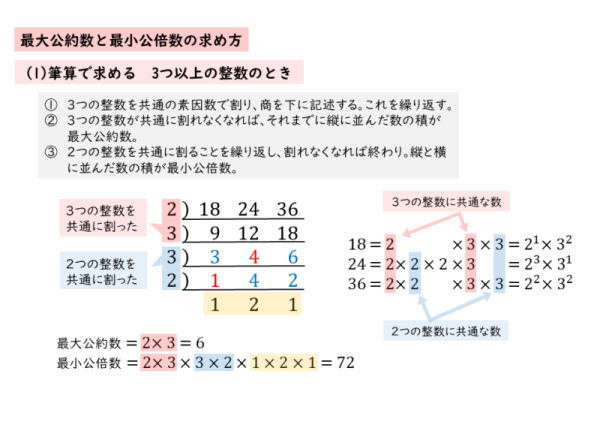
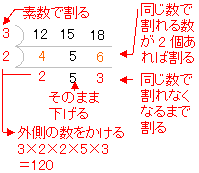
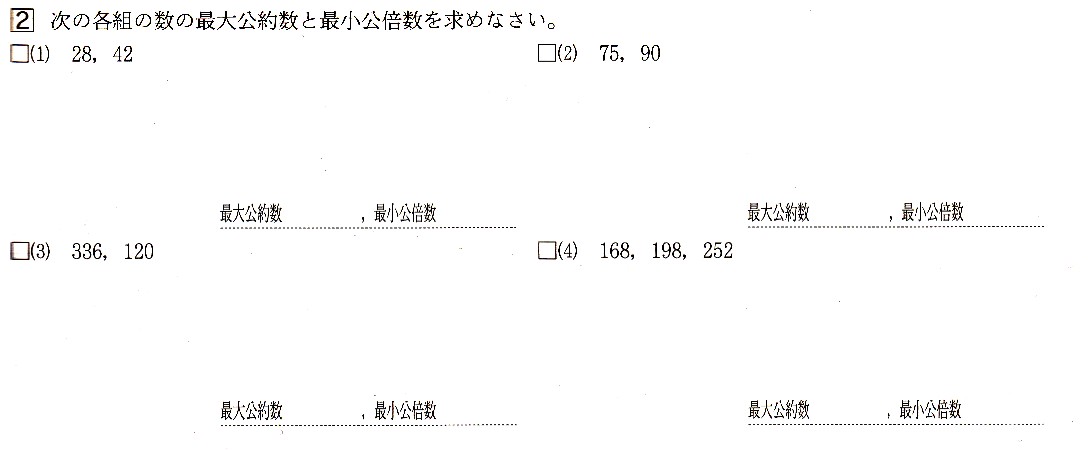
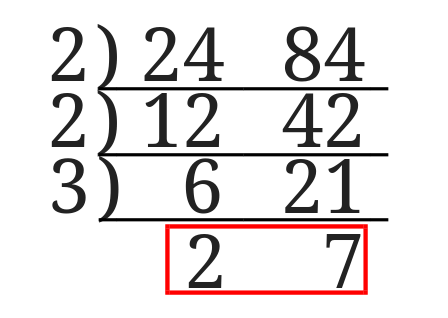
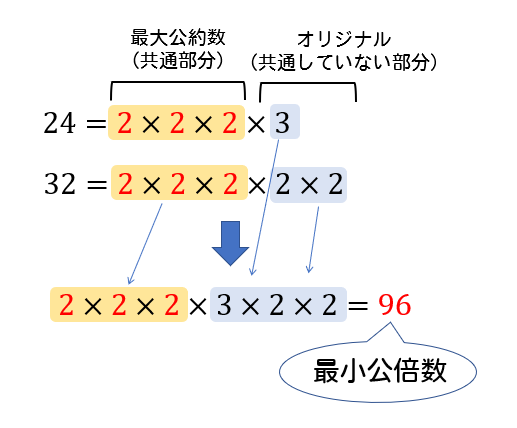
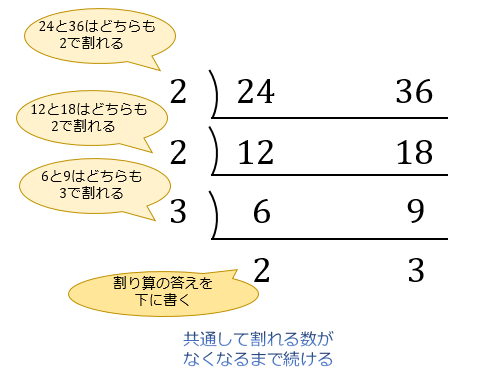
分数 最小 公倍数 問題- 3つの数の数の最小公倍数の簡単求め方 ここでは、 3つの数の最小公倍数 の求め方を解説します。 2つと比べて、ちょっとした テクニックが必要 になりますよ。 12,42,72 の最小公倍数を求めよ。 逆さ割り算 を使って解いていきましょう。 問題文にある 12 最小公倍数は、最大公約数とそれぞれのオリジナル因数を取り出して掛け合わせた値になります。 なので、素因数分解をした式を書き並べ、 それぞれの因数の個数が大きいものを取り出していけばOKです。 答え (1)最大公約数 , 最小公倍数 次に(2)3
分数 最小 公倍数 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
 |  |  |
 | ||
「分数 最小 公倍数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「分数 最小 公倍数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「分数 最小 公倍数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 | ||
「分数 最小 公倍数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
 |  |  |
「分数 最小 公倍数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 | ||
「分数 最小 公倍数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「分数 最小 公倍数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「分数 最小 公倍数 問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
中学受験の算数・理科ヘクトパスカルによる「最大公約数と最小公倍数の問題」の手書き解説です。 ある整数Aと72の最大公約数は12です。これについて,次の問いにこたえなさい。 (1) この2つの整数の最小公倍数が360であるとき,Aはいくつですか。中3 素数·素因数分解 最大公約数·最小公倍数(2) 問題7、問題8、問題9、問題10のhelp 間違っている =>作者: 連絡ありがとう.めったにない変わったエラーでした・・・指数(肩に付ける小さい数字)が地上に降りていましたので訂正しました.
Incoming Term: 最小 公倍数 問題集, 最小 公倍数 最大 公約数 問題, 中学受験 最小 公倍数 問題, 分数 最小 公倍数 問題, 最大 公約数 最小 公倍数 問題集,
コメント
コメントを投稿